|
|
|
|
|
|
 |
|
|

|
 |
|
|
|
|
|
|
 |

|

|

|
 |
|
|
|
|
|
|
|
|
|
|
|
|
Any populations, which show the operation of clear limits on population size, are said to be regulated (Silvertown 1982; p. 110). Population regulation in plants, which are modular organisms, must be discussed as the regulation of biomass rather than numbers (Krebs 1994; p.340). "As a plant population increases in numbers and biomass, either reproduction or survival will be reduced by a shortage of nutrients, water or light; by herbivore damage; by parasites and diseases; or by a shortage of space" (Krebs 1994; p.340). Plants, being fixed in one location, will mainly compete for light or nutrients, and will follow a special rule, the -3/2 power rule or Yoda's law (the self-thinning rule) (Krebs 1994; p.340). This rule, which describes the relationship between individual plant size and density in even-aged populations, tries to fit mortality (thinning) for competition within the population to a theoretical line with a slope of -3/2 (Krebs 1994; p.340). The equation of the self-thinning rule is:
where, ¯m = average plant weight
(grams)
N = plant
density (individuals per square meter)
K = a
constant
The self-thinning rule, which has been suggested as an ecological law
that applies both within one plant species and between different
plant species, highlights the tradeoffs that can occur in organisms
with plastic growth, such that the size of an individual can become
smaller as density increases (Krebs 1994; p.340).
Recent evaluations of this rule have found many exceptions such as
for the gymnosperm trees, which Weller (1987) found that more shade
tolerant tree species had more shallow slopes than the predicted
value (Krebs 1994; p.341). According to Weller, many particular
plants don't fit to the -3/2 predicted slope of the self-thinning
line (only 24/63 fitted to the slope). "The slope of the thinning
line is variable, but this gives us further insight into species
differences under strong competition for light and nutrients" (Krebs
1994; p.340). The relationship between mean plant weight and plant
density expected when total plant biomass is at a maximum, and at a
low density is a slope = -1 (Silvertown 1982; p. 118). "Populations
of small plants at higher densities also increase in mean plant
weight as they grow, but the mortality occurs before the carrying
capacity is reached and before the increase in the total weight of
the plant population ceases" (Silvertown 1982; p. 118). Dense
populations which have reached a size at which mortality occurs
demonstrate a relationship between log mean plant weight and log
density which generally has a slope of -3/2 (Silvertown 1982; p.
118). For as long as the relationship between mean plant weight and
density is governed by a line with a slope of -3/2, total plant
weight will increase because mean plant weight is increasing faster
than density is falling (Silvertown 1982; p. 119).
The weight of plant material that can be obtained from a unit area
planted at a given density (yield) is derived from the -3/2 thinning
law (Silvertown 1982; p. 127). The -3/2 law is:
where, y
= Yield
w = Cd-3/2= mean weight per
plant
d = plant
density
C = interception
of y axis
For a population with a self-thinning line of slope -3/2 and
intercept C, this equation tells us the yield to be expected from a
self-thinning population of density d. For populations which have
reached the upper part of the self-thinning curve where the slope
achieves the value a=1, we obtain a yield/density relationship: y =
C. (Silvertown 1982; p. 127). "Population densities which are high
enough to bring about self-thinning are too high as far as a farmer
is concerned because the casualties of a self-thinning crop are of no
economic value" (Silvertown 1982; p. 127). A straightforward
asymptote relationship is found in various crops where the yield is
measured in terms of whole plant weight or some vegetative part of
this, such as the roots of beet crop or the tubers of a potato crop
(Silvertown 1982; p. 127). Details of the method are given in
Silvertown (1982).
Briefly, increasing density, which can be evenly or unevenly
distributed among the individuals in a population, and intraspecific
(among individuals in a population) competition for a limited
resource has two major effects on the individuals in a population
(Blundon 1994). It can cause mortality directly, or it can lead to
reduced growth rates and fecundity (plastic responses); both mortal
and plastic responses act to reduce population growth rates (Blundon
1994). This experiment was embarked upon the intention to know if
these hypotheses are verifiable and conclusive. The objective of this
experiment was to compare the effects of increasing density and light
intensity on establishment, growth rates, allocation and net
reproduction in an annual and a perennial grass.
January 13 to March 10, 1994, the experiment was conceived in a biology laboratory at Camosun College during a class period. The technique of collecting data and the used material were very simple. In conformity with the tables 1 and 4, the experimentation was divided in two parts, the preparation of the laboratory and the harvest of the plants. During the first week, 20 treatments in a factorial design, containing 2 species (Oats & Bromus), 5 sowing densities (10, 20, 40, 60, and 160 seeds), and 2 light intensities (low and high light), were prepared, and carried in a greenhouse at ambient temperature. After 8 weeks, plants were harvested, dried, weighted (roots and shoots separately), and compiled in the tables 1 and 4. Details of the method are given in Blundon (1994).
Obtained data were compiled in the tables 1 to 4.
Table
1 and table 3 represent data that were compiled by all the groups. In
these tables (Oats and Bromus), there are seed numbers, number of
established plants, total net production or dry weight production
(gr.) divided in roots and shoots, establishment (%), and the
fertility (% of established). The establishment is the percentage of
the number of established plants in function of sowing densities. The
fertility (% of established) was abandoned because plants were not
old enough to produce flowers. Table 2 and table 4 are the average of all data that were compiled in
table
1 and table 3.
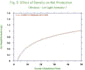
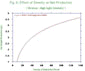
Figure
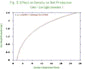
1 and figure 2 represent the effect of density on establishment success.
The number of established plants in function of the seed number was
plotted for each species, with both light intensities. Fig. 1 and fig.
2 show two different curves, a straight
line and a logarithmic (maybe a sigmoid) curve. Oats and Bromus
curves are logarithmic curves at low light intensity and straight
lines at high intensity. Consequently, the mortality rate is higher
at low light intensity than at high light intensity. The Oats
mortality is higher than Bromus mortality.
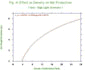
Figure
3, figure 4, figure
5, figure 6 show the effect of density on total quantity of net
production by each population. The dry weight production in function
of density of established plants for both species was plotted for
each species and each light intensity. Oats and Bromus curves are
logarithmic curves at both intensities. Consequently, at the
beginning, net production increases continuously with increasing
density, but at the end, each curves has a straightforward asymptote.
The response is the same for both light intensities, but the dry
weight production rate at low light intensity is lower than at high
light intensity. The Bromus dry weight production rate is lower than
the Oats dry weight production rate.
Figure
7, figure 8, figure
9, figure 10 show the effect of increasing density on the average
weight of individuals in each population. The total net production
was divided by the number of established plants in each population,
and a graph log-log, containing this division, was plotted in
function of the density. The results of each curve are a straight
line, but a logarithmic curve was drown to know the exact formulas.
Contrary to others that have a negative straight line, Oats at low
light intensity has a straight line equal to zero. The growth of
individuals of Oats is more suppressed by increasing densities than
Bromus. Oats at low light intensity doesn't seem to be affected by
the competition, while Oats a high light intensity seems to be the
most affected by the competition. In general, at low light intensity,
the competition is low, while at high light intensity, the
competition is more important. With our data, there is any
relationship between root and shoot ratios.
According to the initial hypotheses, this
experiment seems to be very conclusive and verifiable. The numerous
figures show the direct effects of the population regulation. Despite
of the fact that intraspecific competition has few effect at low
light intensity, it decreases the population growth rate and causes
mortality directly. Unfortunately, it was impossible to conclude
something about the fecundity and the relationship with root and
shoot ratio. Because plants were too young, the fecundity was
indeterminable. The -3/2 power rule or Yoda's law wasn't conclusive
because most plants have a slope near 0. This experiment was directly
in accordance with Silvertown who said: "populations of small plants
at higher densities also increase in mean plant weight as they grow,
but the mortality occurs before the carrying capacity is reached and
before the increase in the total weight of the plant population
ceases." A straightforward relationship was found too where the yield
is measured in terms of whole plant weight. At low intensity, the
competition is low or absent, while at high intensity, the
competition is high and more affected by the processes of regulation.
Oats is the less and the most affected by the competition and the
processes of regulation, dependent of the light intensity. There was
some problems with the plants pots, because some roots could reach
directly the water outside of the pot, and by this fact escape to the
competition. An interesting improvement of this method should be to
buy better oats seeds and try to find a better solution to eliminate
the contact between roots and water outside of the pot.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
 |
|
|
|
|
|
|
 |
 |
|
|
|
|
|
|
 |
 |
|
|
|
|
|
|
 |
 |
|
|
|
|
|
|
 |
 |
I would like to thank my classmate Jason, who helps me to do this experiment and all students in my class that contributed to the success of this experiment. I would like particularly thank Dr, David J. Blundon for his precious help and for its laboratory manual in which I took a lot of information and ideas.
Blundon, David J. 1994. Ecology: Laboratory Manual. Camosun College, Victoria, Canada.
Krebs, Charles. J. 1994. Ecology. HarperCollins College Publishers, New York, USA.
Silvertown, Jonathan W. 1982. Introduction to Plant Population Ecology. Longman Group Limited, New York, USA.